


Next: if statements
Up: Fundamental constructions of F77
Previous: do-enddo loops
In the preceding section we learned that the statement inside the do-enddo loop is
being executed while the controlling parameter lies betwen the specified initial and final
value. Remember that the decision about the execution of the statements inside the
do-enddo construction is made before each individual loop.
A similar construction which is frequently used in Fortran codes is the do while-enddo
loop. The body of the loop is executed provided that the logical expression written behind
while is true. At the end of each cycle the program returns back to the do while
header and again checks the validity of the logical expression. This process occurs until the
condition becomes false and the program continues below enddo. The standard
do while-enddo loop looks as follows:
do while (logical expression)
:
statements
:
enddo
The do while-enddo loops are mainly used once you want to ensure that a particular loop will
be executed at least once. In numerical mathematics, this frequently occurs in the algorithms for
finding roots of functions where you always start with an initial guess and converge towards the
configuration corresponding to zero functional value. The whole algorithm exits once you achieve a
sufficient accuracy, i.e. once the functional value lies within a given 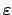 -neighborhood
of zero. To demonstrate the use of these
-neighborhood
of zero. To demonstrate the use of these do while-enddo loops, look at the following simple
problem.
Problem: Write an algorithm which finds one root of function
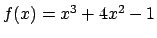 using a
bisection method. Search the interval
using a
bisection method. Search the interval
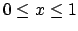 which definitely contains a root and
obtain the solution with accuracy
which definitely contains a root and
obtain the solution with accuracy
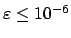 .
.
Solution:
eps = 1.0e-6
xleft = 0.0
xright = 1.0
fmid = eps+1.0 ! execute the first cycle
do while (ABS(fmid) .gt. eps)
xmid = (xleft+xright)/2.0
fleft = xleft**3 + 4*xleft**2 - 1
fmid = xmid**3 + 4*xmid**2 - 1
fright = xright**3 + 4*xright**2 - 1
if (fleft*fmid .le. 0) then
xright = xmid
else
xleft = xmid
endif
enddo
write(*,'("Root is x = ",F8.6)') xmid
Initially, we set the requested accuracy in eps and specify the interval in which we are
going to seek the solution. The first run of the do while-enddo loop calculates the position
of the middle point and determines the functional values for the boundary of the interval and this
middle point. The root can then lie either in the interval (xleft,xmid), provided that
fleft and fmid are of opposite signs, or in the interval (xmid,xright) if
fmid and fright are of opposite signs. This new interval is then bisected and the loop
repeats until the functional value corresponding to the middle point xmid lies in the
eps-neighborhood of zero. When this happens, the execution of the do while-enddo loop is
stopped and we get the result: Root is x = 0.472834.
The algorithm above calculates the functional values at xleft and xright at the
beginning of each cycle, although this is not necessary in subsequent cycles of the loop. Try
to understand the algorithm in more detail and improve the program to avoid these unnecessary
operations. Remember that the functional value at xmid has to be calculated in each cycle.



Next: if statements
Up: Fundamental constructions of F77
Previous: do-enddo loops
Roman Groger
2004-09-27