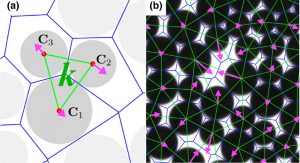
Pink arrows point from the center of a particle to the center of the blue polygonal cell in which it resides {actual size in (a); elongated by x8 in (b) for clarity}. These arrows tend to point toward open/under-packed regions and away from close-packed regions. This is the basis for a new and widely-applicable method to characterize structural defects in disordered materials.
Douglas Durian and Andrea Liu
Disordered packings like sand piles and metallic glasses have arrangements of their constituent particles that appear very similar to those of a liquid. It is a very hard and long-standing problem to be able “look” at the particle arrangement and tell if the the system is rigid, and where flow will initiate if the system is deformed.
One key concept has been that of “free volume” — the idea that regions that are underpacked are more vulnerable to rearrangement than overpacked ones. However, it has been difficult to identify underpacked regions from experimental images without introducing thresholds and in a way that is valid for systems with interactions that are not either infinitely-repulsive or zero.
We made major progress on this issue in Ref.[1] by devising a new tool based on the pink arrows shown in the accompanying figure. These identify the under-packed weak regions, without the usual need to calibrate a threshold. We also showed how the tool can be used to structurally identify the transition from liquid-like to solid-like behavior that occurs with increasing particle concentration.
[1] J. M. Rieser, C. P. Goodrich, A. J. Liu, and D. J. Durian, “Divergence of Voronoi cell anisotropy vector: A threshold-free characterization of local structure in amorphous materials”, Phys. Rev. Lett. 116, 088001 (2016).
Technically, our new measure is equal to the divergence Qk of the vector field (pink arrows) pointing from the center of each particle to the centroid of its Voronoi cell (blue polygons). This is computed numerically for each triangle (green) in the dual Delaunnay triangulation. Statistically, we find that Qk is proportional to the local free area. But crucially Qk can be both positive and negative — the former for overpacked regions and latter for underpacked regions; therefore, only the sign of Qk is needed, without the use of an arbitrarly threshold, to tell where defects may be. Furthermore, the distribution of Qk values is found to be nearly Gaussian – like a random variable – but with a small power-law tail on the underpacked side. This strongly helps identify anomalously underpacked regions. This new tool is applicable to amorphous materials ranging from atomic and molecular glasses, to nanoparticle and colloidal systems, as well as macroscopic grains.
