L. J. Daniels, T. K. Haxton, N. Xu, Andrea J. Liu and Douglas J. Durian
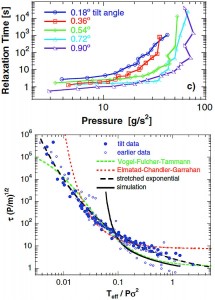
Figure 1. (a) Uncollapsed data for relaxation time vs. pressure. (b) Collapsed data for dimensionless relaxation time vs. inverse dimensionless pressure.
Amorphous liquids behave as mechanically rigid solids on time scales below the relaxation time, which grows unbearably long as the temperature is lowered or as the pressure is raised. These two pathways to the glass transition are equivalent for the system of thermal hard spheres. Dimensional analysis suggests that the relaxation time τ , made dimensionless as τ (Pσd-2/m) ½ by pressure P, sphere diameter σ, and sphere mass m, must depend only on the dimensionless ratio T/Pσd, where T is temperature, and d is dimensionality. Thus, the dimensionless relaxation time increases in exactly the same way whether T is lowered or P is raised, and depends only on the ratio of the thermal energy to the pressure-volume needed to open up a hole of the same order as the particle size.
We conducted experiments [1] in which spheres roll stochastically due to turbulence in a uniform upflow of air. Here the relaxation time grows as the air flow is decreased or pressure is raised. The thermal energy of the beads is negligible compared to their kinetic energy, which corresponds to a well-defined effective temperature Teff [2]. Pressure is applied by tilting the sample, and is the projected weight per length as required for hydrostatic equilibrium.
Remarkably, the dimensionless relaxation time for this granular system depends only on the ratio of Teff to the pressure-volume work needed to open up a hole of the order of the particle size, just as for thermal hard spheres. Thus, the effect of pressure, a mechanical load, is directly related to the effect of kinetic energy supplied by driving the system via air flow.
[1] Phys. Rev. Lett. 108, 13008 (2012)
[2] Phys. Rev. Lett. 101, 245701 (2008)
