Kerstin N. Nordstrom, Emilie Verneuil, Jerry P. Gollub, and Douglas J. Durian
Many fluids of practical importance (paint, milk, etc.) are suspensions of particles. The flow properties of such suspensions depend dramatically on the particle properties, such as their softness, especially when their concentration is high. Yet reliable ways of measuring the elastic properties of suspended colloidal particles are scarce. We have developed a novel way to determine the elastic modulus of suspended soft particles by spinning the fluid in a centrifuge and observing the apparent volume change of the solid phase.
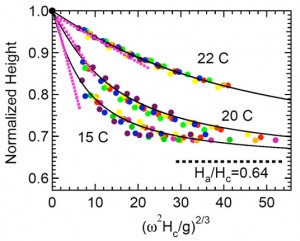
Our suspension consists of ~1 micron NIPA microgel particles, synthesized in the Yodh group at Penn. When the suspension is spun at high rotation rate in a capillary tube, the enhanced effective gravity causes the particles to deform as they are compressed into a packed configuration, leaving an interface between the solid and liquid phases. We measure the height of the solid phase as a function of rotation rate, as shown in Fig. 1(a). The asymptotic height decline to 0.64 of the initial height tells us that the particles deform to fill all of the available space, but without expelling fluid from the interior of the particles. We fit the decline to a theory we have devised, based on the hypothesis that the particles behave like ordinary deformable spheres at small deformation, and that the compressive stress diverges when the particles are space filling. We are able to extract the bulk elastic modulus of the particle layer, and then extract the elastic modulus of the individual particles (Fig. 1b) as their size is varied by modifying the temperature of the sample, even though they are only about 1 micron in diameter. This information is critical to understanding the jamming and flow properties of dense suspensions.
a) Height as a function of rotation rate; Hc = height of sample when fully packed; g = 9.8 m/s2.
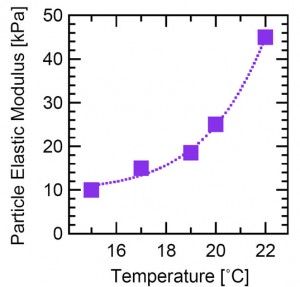
b) Particle elastic modulus as a function of temperature. Particles shrink when heated, and stiffen.